〜 3 Dの世界へようこそ!柱と三角帽子の面積・体積計算〜
こんにちは、Thumb up Cafe Blog へようこそ!
中学の図形では、平面(ペラペラな紙)だけでなく、タテ・ヨコ・高さがある「空間図形(立体)」を習います。立体は、**「どれくらいの大きさ(体積)」と「どれくらいの紙で包めるか(表面積)」**を求めることが大事です。
今日のカフェでは、立体図形の超重要な 2 つの仲間と、立体ならではの**「ねじれの位置」**という考え方をマスターしましょう!
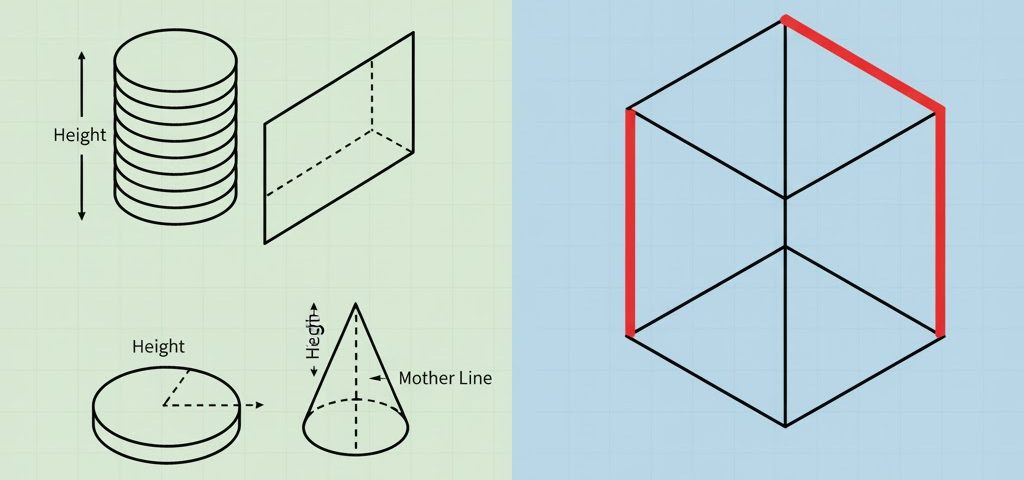
1. 立体の 2 大スター:柱体と錐体
立体図形は大きく分けて 2 つのグループに分けられます。
🌟 仲間 1:柱体(ちゅうたい) → 「まっすぐな箱」
底面が 2 つあり、その 2 つの底面が平行で、側面がまっすぐ(垂直)になっている立体です。
- 例: 鉛筆の箱、トイレットペーパーの芯(円柱)、三角柱
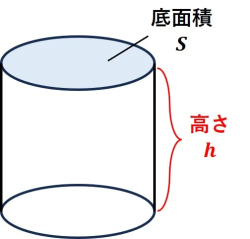
💡 柱体の「体積」と「表面積」
| 求めるもの | 公式 | イメージ |
|---|---|---|
| 体積 (V) | (底面積) × (高さ) | 底面を積み重ねた「積層(せきそう)」のイメージです。 |
| 表面積 (S) | (底面積 × 2) + (側面積) | 上と下のフタ 2 枚と、胴体部分の紙 1 枚(展開図)。 |
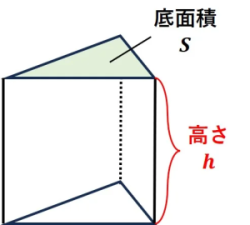
🌟 仲間 2:錐体(すいたい) → 「三角帽子」
底面が 1 つだけで、側面が 1 点(頂点)に集まっている、とがった立体です。
- 例: 三角コーン(円錐)、ピラミッド(四角錐)、三角錐
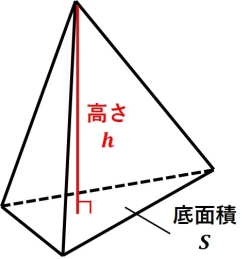
💡 錐体の「体積」と「表面積」
| 求めるもの | 公式 | イメージ |
|---|---|---|
| 体積 (V) | (底面積) × (高さ) ×1/3 | 同じ底面・高さの柱体のちょうど 3 分の 1 になります!なぜ 1/3 かは高校で学びます。 |
| 表面積 (S) | (底面積) + (側面積) | 底面 1 枚と、胴体部分(側面積) 1 枚(展開図)。 |
2. 【超重要】円錐(えんすい)の側面積を求める裏ワザ
錐体の中で特に重要なのが、三角コーンの形をした円錐です。円錐の側面積(胴体部分の面積)を求めるには、展開図で現れる**「おうぎ形」**の面積を求めなければなりません。
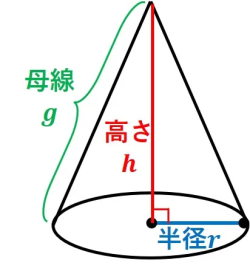
㊙️ 円錐の側面積の求め方
円錐を広げたおうぎ形の面積は、次の 2 つの数字だけで簡単に求められます。
- 母線(ぼせん):おうぎ形の半径になる、円錐の斜めの線( g とする)。
- 底面の半径:円錐の底の円の半径( r とする)。
側面積 = π × 母線(g) × 底面の半径(r)
3. 立体ならではの発見:「ねじれの位置」
立体図形には、平面図形にはない特別な位置関係があります。それが「ねじれの位置」です。
【定義】
空間の中で、
- 交わらない
- 平行でもない2 つの直線の関係のこと。
💡 ねじれの位置のイメージ
教室の**「天井の 1 本の線」と「床の 1 本の線」**で考えてみましょう。
- 交わる例: 天井の 2 本の線は、角で交わります。 → ねじれの位置ではない
- 平行な例: 天井の線と、床のその真下にある線は平行です。 → ねじれの位置ではない
- ねじれの位置の例:
- 天井の右奥の線と、床の手前の線(自分に近い線)。
- これらは、平行でもないし、どこまで伸ばしても交わりません。これが「ねじれの位置」です!
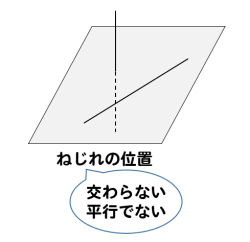
ねじれの位置は、** 3 次元( 3 D)の立体の中でしか成り立たない、特別な関係**だと覚えておきましょう。
🌟 まとめと次のステップ
空間図形は、**「展開図」**を頭の中で想像できるようになれば 9 割は解けます。そして、公式の 1/3 とねじれの位置は、確実に押さえておきましょう。

コメント