〜算数の「□」から「 x 」へ!バランスゲームで考える計算の魔法〜
こんにちは、Thumb up Cafe Blog へようこそ!
中学の数学で「方程式(ほうていしき)」を習うと、算数で使っていた「□(しかく)」が「 x 」という文字に変わります。方程式の目的はただ一つ、**「 x に当てはまる数字を見つけること」**です。
今日のカフェでは、方程式を解くための 2 つの強力なルール、「移項(いこう)のルール」と「比例式のルール」を、バランスゲームのように簡単に解説します!
1. 一次方程式の解き方:魔法のルール「移項」
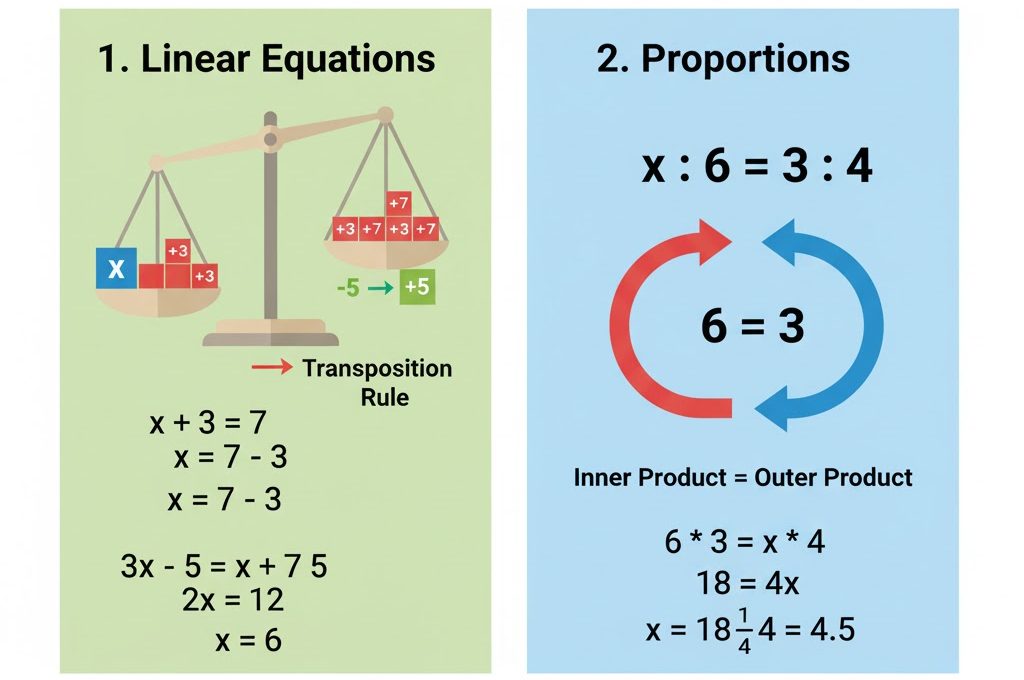
一次方程式は、**「左と右が釣り合っている天秤(てんびん)」**をイメージしてください。左側(左辺)と右側(右辺)は、**必ず同じ重さ(値)**になっています。
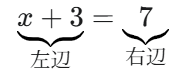
💡 ゴールは「 x = 答え 」の形!
最終的なゴールは、左辺に x だけ、右辺に数字だけがある x = (答え) の形にすることです。
【ルール 1】移項(いこう):符号を変えてお引越し!
方程式を解くための魔法が「移項」です。項(たし算・ひき算で区切られたカタマリ)を、等号(=)をまたいで反対側に移動させることです。
移項のルールは簡単です。
「$=$(イコール)をまたぐとき、プラスとマイナス(符号)を逆に変える!」
| 移動前 | 移動後 | 理由(天秤で考える) |
|---|---|---|
| +3 を右へ移項 | → -3 | 左の皿から +3 を取り除いたら、釣り合わせるために右の皿からも +3 を取り除く(つまり 3 をひく)のと同じ。 |
| -2x を右へ移項 | → +2x | 左の皿にあった -2x を消すために +2x を足したら、右の皿にも +2x を足すのと同じ。 |
【解き方の手順】
3x – 5 = x + 7 を解いてみましょう。
- ** x の項を左辺に、数字の項を右辺に集める** (移項する)。
- 左辺の -5 を右辺へ →+5
- 右辺の +x を左辺へ →−x
- 3x – x = 7 + 5
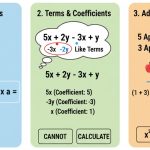
- 両辺を計算する(同類項をまとめる)。
- 2x = 12
- ** x の係数で両辺を割る**。
- x = 12 ÷ 2
- x = 6
2. 比例式の解き方:内側と外側をかけ算!
比例式は、**「算数の比( 2:3 など)」**が等号(=)で結ばれた式です。

【ルール 2】比例式のルール:内項の積と外項の積
比例式では、次のルールが必ず成り立ちます。
内側の数字同士をかけたもの(内項の積)と、外側の数字同士をかけたもの(外項の積)は、必ず等しくなる!
内側の積 = 外側の積
b × c = a × d
【解き方の手順】
x : 6 = 3 : 4 を解いてみましょう。
- 内側同士と外側同士をかけ算で結び、等号でつなぐ。
- 内側( 6 と 3 ) → 6 × 3 = 18
- 外側( x と 4 ) →4 × x = 4x
- 4x = 18
- 一次方程式として解く( x の係数で割る)。
- x = 18 ÷ 4

🌟 まとめと次のステップ
方程式は、複雑そうに見えても、この 2 つのルールさえ守れば、必ず x の値を見つけ出すことができます。
| 式の種類 | 解くためのルール | 使い方 |
|---|---|---|
| 一次方程式 | 移項 | = をまたぐとき、符号を逆に変える。 |
| 比例式 | 内項の積 = 外項の積 | 外側同士、内側同士をかけて一次方程式に直す。 |
何度も練習して、これらのルールを「考える前」に体が動くレベルまでマスターしましょう!
🚀 ブログだけでは物足りない、個別最適な学習サポートが必要な方へ
Thumb up Cafe のオンライン個別指導では、文章問題からの「立式(方程式を作ること)」も含めて、 1 対 1 で丁寧に指導し、方程式を得点源に変えていきます。
コメント