🚀 【中学数学のスタート！】正の数と負の数マスター講座！

〜お金とお天気で理解する、新しい数の世界〜

こんにちは、Thumbs up Cafe Blog へようこそ！

中学に入ると、数学で最初に「正の数（プラスの数）」と「負の数（マイナスの数）」という新しい友達に出会います。この「マイナスの数」がわかれば、数学は一気に楽しくなりますよ！

今日のカフェでは、このプラスとマイナスの数の計算のルールと、ちょっと変わった**「絶対値」**という考え方を、誰でもわかるように解説します。

---

1. なぜ「マイナスの数」が必要なの？

私たちは普段の生活で、すでにマイナスの数を使っています。

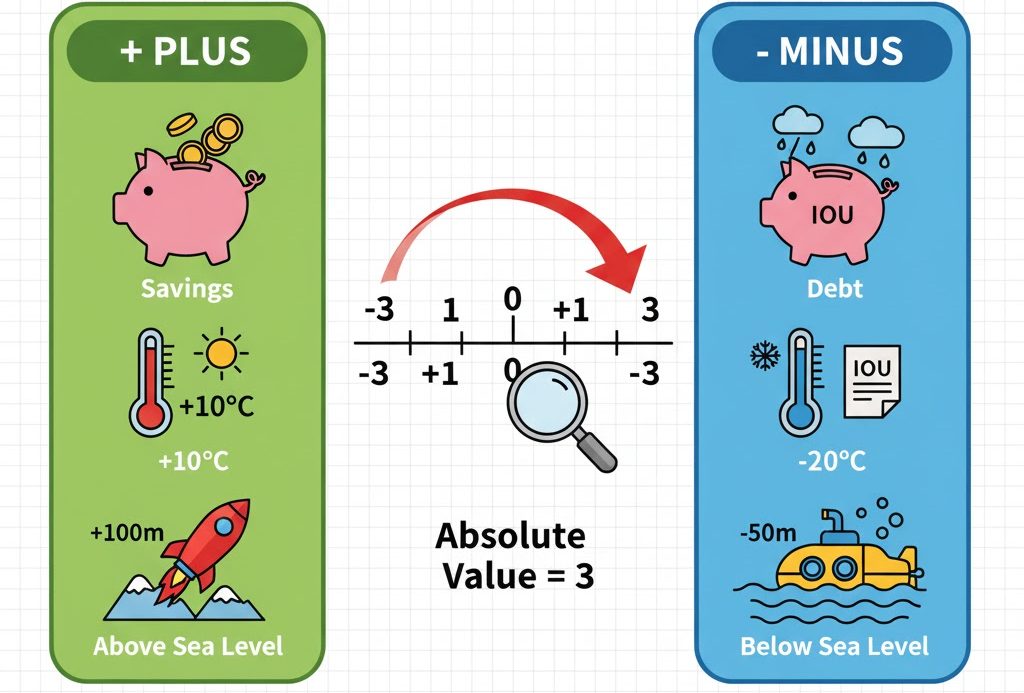
状況	プラスの数 (+)	マイナスの数 (-)
お金	貯金（手元にお金が増える）	借金（手元のお金が減る）
温度	** 0℃ より高い**温度	** 0℃ より低い**温度（氷点下）
基準点	基準点より上や右	基準点より下や左

数学では、この**「逆の方向や状態」**を表すために、数字の前に「－ (マイナス)」をつけます。

• 正の数： 5 や +5 （プラスは省略されることが多い）
• 負の数： －5（マイナスは絶対に省略できない）

---

2. 絶対値： 0 からの「道のり」

まず、とても大切な「絶対値」という言葉を覚えましょう。

【絶対値のルール】

絶対値とは、「 0 (ゼロ)からの道のり（距離）」のことです。

数直線上で考えてみましょう。

• ** +5 の絶対値：** 0 から +5 までの道のりは 5 です。 →　5
• ** －5 の絶対値：** 0 から －5 までの道のりも 5 です。 →　5

道のりにマイナスはありませんよね？だから、絶対値は必ずプラスの数か 0 になります。

---

3. 正負の数の四則計算マスター！

いよいよ計算のルールです。これがわかれば、中学数学の最初でつまずくことはありません！

3-1. たし算（加法）と ひき算（減法）

たし算とひき算は、**「仲間（符号が同じ）」か「敵（符号が違う）」**かで考えます。

① 仲間（符号が同じ）の計算ルール

符号が同じ数の場合は、そのまま絶対値（道のり）をたし算し、共通の符号をつけます。

式の例	お金で考えると…	計算の仕方	答え
(+3) + (+5)	3 円貯金して、5 円貯金した。	3+5=8	+8
(-3) + (-5)	3 円借金して、5 円借金が増えた。	3+5=8	－8

② 敵（符号が違う）の計算ルール

符号が違う数の場合は、絶対値が大きい方から小さい方をひき算し、絶対値が大きい方の符号をつけます。

式の例	お金で考えると…	計算の仕方	答え
(+8) + (-5)	8 円貯金があるけど、5 円借金した。	8-5=3	+3
(-8) + (+5)	8 円借金があるけど、5 円貯金した。	8-5=3	－3

---

3-2. かけ算（乗法）と わり算（除法）

かけ算とわり算は、数字を計算した後、マイナス（ － ）の数がいくつあるかで符号を決定します。

【符号の決定ルール】

マイナスの数 ( － ) の個数	答えの符号
偶数個（ 0 個、 2 個、 4 個 … ）	プラス（ + ）
奇数個（ 1 個、 3 個、 5 個 … ）	マイナス（ － ）

① かけ算の例

式の例	マイナスの個数	答えの符号	答え
(+4) × (+2)	0 個 (偶数)	+	+8
(－4) × (+2)	1 個 (奇数)	－	－8
(－4) × (－2)	2 個 (偶数)	+	+8

② わり算の例

わり算も同じルールです。

式の例	マイナスの個数	答えの符号	答え
(+10) ÷ (－5)	1 個 (奇数)	－	－2
(－10) ÷ (－5)	2 個 (偶数)	+	+2

---

🌟 まとめと次のステップ

正の数・負の数の計算は、慣れるまでは混乱しやすいですが、**「符号のルール」**さえ間違わなければ大丈夫です。

計算の種類	符号の決め方
たし算・ひき算	絶対値の大きさを比べ、絶対値が大きい方の符号をつける。
かけ算・わり算	マイナスの個数を数え、偶数なら +、奇数なら －。

この土台をしっかりと固めることが、この先の中学数学（文字式、方程式、関数）をスムーズに進めるためのカギとなります。

---

🚀 ブログだけでは物足りない、個別最適な学習サポートが必要な方へ

Thumbs up Cafe のオンライン個別指導では、このような「最初のつまずきやすい単元」を、お子様のペースに合わせて徹底的に反復練習し、数学を得意科目に変えていきます。