こんにちは、Thumb up Cafe Blogへようこそ!
中学3年生の図形分野で学ぶ「円の性質」は、中学校で学ぶ図形知識の総仕上げです。円の性質を理解すると、複雑な図形の中の隠された角度や垂直な関係が簡単に見抜けるようになります。
今回は、円の性質の中でも最も重要で強力なルールである「円周角の定理」と、円と直線の美しい関係を示す「接線の性質」の基礎を徹底解説します!
1. 🌈 円周角の定理: 中心角との特別な関係
1-1. 円周角と中心角の定義
円の性質を語る上で、まず2つの角を区別して覚える必要があります。どちらも「弧(こ)」(円周の一部)から作られる角です。
- 中心角(ちゅうしんかく): 弧の両端と、円の中心を結んでできる角。
- 円周角(えんしゅうかく): 弧の両端と、円周上の点を結んでできる角。
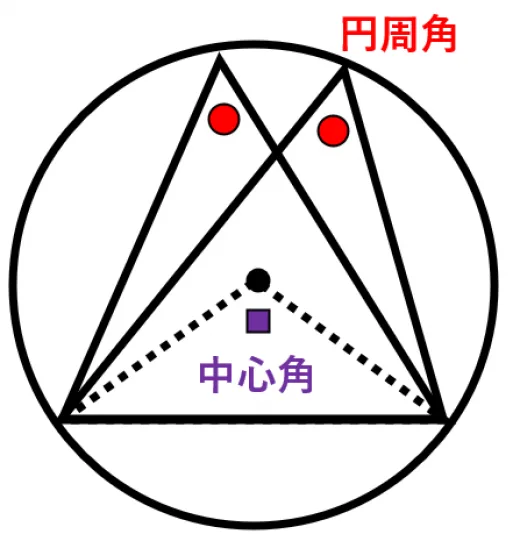
1-2. 🔑 円周角の定理(基本)
円周角の定理は、この2つの角の間に成り立つ絶対的なルールです。
一つの弧に対する円周角の大きさは、その弧に対する中心角の大きさの1/2である。
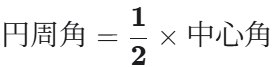
- 例: 中心角が 100° なら、それに対する円周角は必ず 50° になります。
1-3. 🔑 円周角の定理(応用)
基本の定理から、次の2つの重要な応用ルールが導かれます。
1. 同じ弧に対する円周角は等しい

一つの弧に対する円周角は、円周上のどの位置に点をとっても、その大きさはすべて等しくなります。なぜなら、中心角の半分だからです。
2. 半円の弧に対する円周角は 90°(直角)である
円の中心を通る直径は、円周をちょうど半円に分けます。
- 半円に対する中心角は、直線なので 180° です。
- したがって、半円に対する円周角は、 180° × 1/2 = 90° になります。
2. 📏 接線と半径の関係: 隠れた垂直を探せ!
2-1. 接線(せっせん)と接点(せってん)
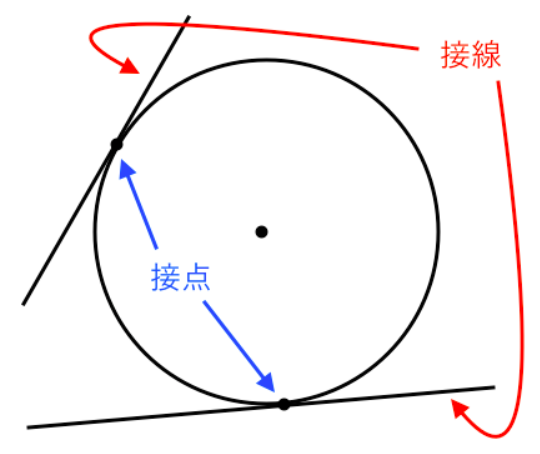
- 接線: 円とただ一点でのみ接する直線。
- 接点: 円と接線が接している、そのただ一つの点。
2-2. 🔑 接線と半径の定理
接線と半径の間には、図形の問題を解く上で非常に強力な関係が成り立ちます。
円の接線は、接点を通る半径と、必ず垂直に交わる。
接線 ⊥ 半径
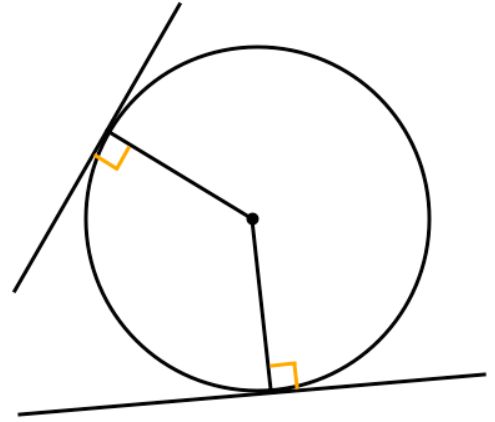
- ポイント: 接点から円の中心に向かって線を引くと、必ずそこに90°(直角)が生まれます。問題で接線が出てきたら、90° の隠れた直角三角形を探すのがセオリーです。
2-3. 🔑 円外の点から引いた接線の長さ
円の外のある点から円に2本の接線を引くとき、その2本の接線の長さにはルールがあります。
円外の一点から円に引いた2本の接線の長さは等しい。
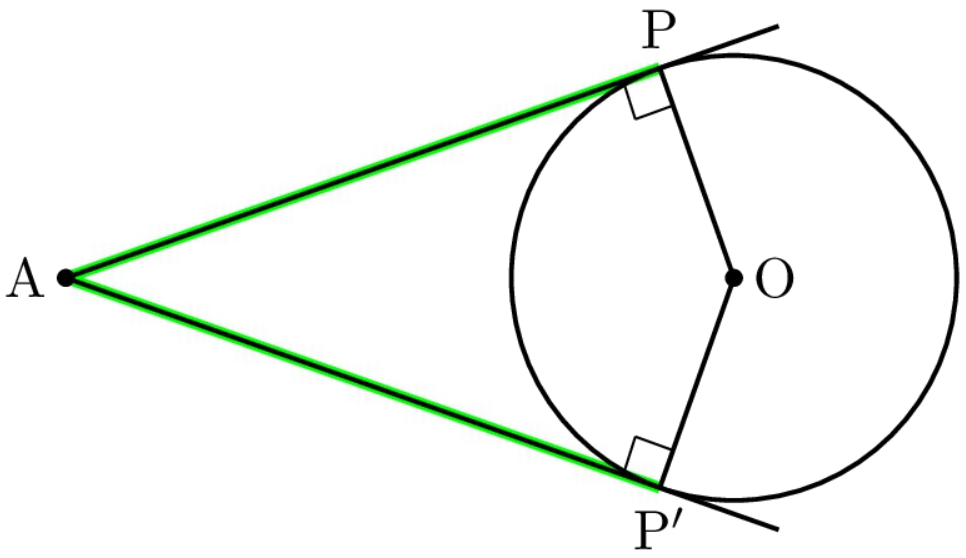
(AP=AP’)
- 例: 点 A から円に引いた接線の接点をそれぞれ P、P’ とするとき、AP = AP’ が成り立ちます。
- このとき、接線と半径の定理と合わせると、△ APO と △ AP’O (O は円の中心)は合同な直角三角形になります。
3. 🎯 Thumb up Cafe の個別指導で図形の応用力を高める!
円の性質は、円周角の定理と接線の性質から生まれる 90° や等しい角をいかに見つけ出すかが勝負です。これらの定理は、この後で学ぶ三平方の定理と組み合わせて、難易度の高い入試問題でも頻繁に使われます。
🚀 ブログだけでは物足りない、個別最適な学習サポートが必要な方へ
Thumb up Cafe のオンライン個別指導では、
- 円周角の定理を使った、四角形が円に内接する条件など応用問題へのステップアップ
- 接線と半径の関係から直角三角形を見つけ出し、三平方の定理へつなげる思考回路の訓練
- 補助線を必要とする、複雑な円の図形問題の解法パターン演習
などを 1 対 1 で徹底指導し、図形分野を得点源に変えていきます。
「円周角と中心角の関係をすぐ忘れてしまう…」「接線が 90° になることが計算に活かせない…」という方は、ぜひ一度ご相談ください!



コメント