こんにちは、Thumb up Cafe Blogへようこそ!
中学数学で最も重要で、最も広く応用される定理が「三平方の定理(さんへいほうのていり)」です。別名「ピタゴラスの定理」とも呼ばれ、直角三角形の辺の間に成り立つ、絶対的なルールを示しています。
この定理をマスターすれば、見えない長さや空間図形の中の距離まで計算できるようになります。今回は、三平方の定理の基本から、応用範囲までを徹底解説します!
1. 🌈 三平方の定理の定義: a² + b² = c²
1-1. 定理が成り立つ条件
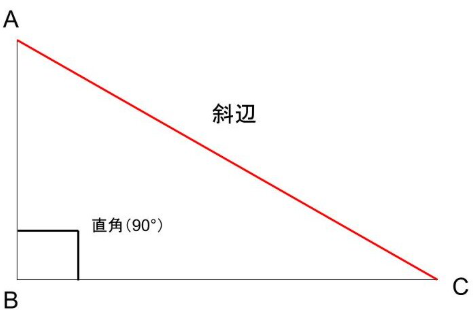
三平方の定理は、直角三角形にのみ成り立ちます。
- 直角三角形: 1つの角が 90°(直角)である三角形。
- 斜辺(しゃへん): 直角と向かい合っている最も長い辺。
- 他の2辺: 直角を挟む2辺。
1-2. 🔑 三平方の定理の基本公式
直角三角形において、直角を挟む2辺の長さを a と b、斜辺の長さを c とするとき、次の関係が成り立ちます。
a² + b² = c²
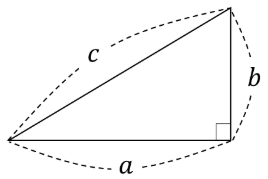
(直角を挟む辺)² + (直角を挟む辺)² = (斜辺)²
【例】
直角を挟む2辺の長さが 3cm と 4cm の直角三角形の斜辺の長さを x とすると、
3² + 4² = x²
9 + 16 = x²
25 = x²
x = 5 (長さなので x > 0 )
2. 🔑 辺の長さで直角三角形を判定!
三平方の定理は、辺の長さがわかっている三角形が直角三角形であるかどうかを判断するのにも使えます。これを「三平方の定理の逆」と呼びます。
三平方の定理の逆:
ある三角形の最も長い辺の2乗が、他の2辺の2乗の和に等しいとき、その三角形は直角三角形である。
【例】
3辺の長さが 5cm、 12cm、 13cm の三角形は直角三角形か?
- 最も長い辺(斜辺の候補): 13
- 計算:
- 他の2辺の2乗の和: 5² + 12² = 25 + 144 = 169
- 最も長い辺の2乗: 13² = 169
- 結論: 5² + 12² = 13² が成り立つので、この三角形は直角三角形であると言えます。
💡 ピタゴラス数
三平方の定理が成り立つ整数の組 (a, b, c) を「ピタゴラス数」と呼びます。
- (3, 4, 5)
- (5, 12, 13)
- (8, 15, 17)
これらを覚えておくと、計算が大幅にスピードアップします。
3. 🧩 空間図形への応用: 奥行きを測る!
三平方の定理の真価は、空間図形(立体)の中の長さを求められることにあります。これは、「求める線分を含む直角三角形」を空間の中に見つけ出すことがカギです。
3-1. 直方体・立方体の対角線
立方体や直方体の辺の上や面の上に直角三角形を見つけ、三平方の定理を2回使って、空間を斜めに貫く対角線の長さを求めます。
【例】
たて 3、よこ 5、高さ 4 の直方体の対角線 EC の長さ L を求める。
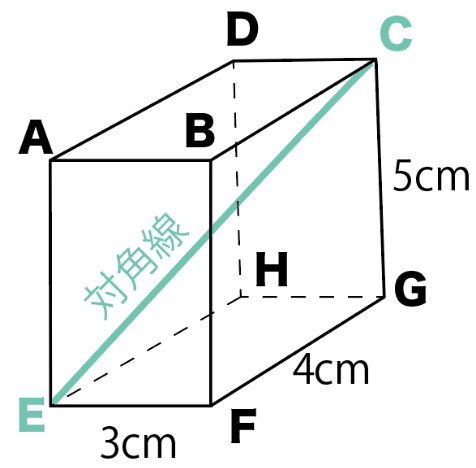
- 底面の対角線 EG を求める: △ EFG で 3² + 4² = EG² → EG = 5
- 空間の対角線AG を求める: △ EGC は直角三角形(∠ C = 90°)
EG² + CG² = EC²
5² + 5² = L²
25 + 25 = 50
L = √50 = 5√2
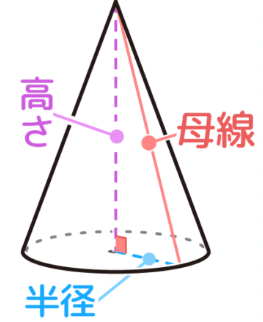
3-2. 円錐の高さ(展開図と斜辺)
円錐の高さ h を求めるときにも使われます。円錐の側面の母線の長さが斜辺となり、底面の半径と高さが他の2辺となります。
- (半径)² + (高さ)² = (母線)²
4. 🎯 Thumb up Cafe の個別指導で応用問題を突破!
三平方の定理は、二次方程式や円の性質、相似といった他の分野と組み合わさって出題されることが非常に多いです。「直角三角形をいかに素早く見つけ出すか」が点数に直結します。
🚀 ブログだけでは物足りない、個別最適な学習サポートが必要な方へ
Thumb up Cafe のオンライン個別指導では、
- 直角三角形の探し方(補助線の引き方、空間図形での見方)の徹底トレーニング
- 平方根の計算と定理をミスなく組み合わせる演習
- 正四角錐の高さや最短距離など、難易度の高い空間図形応用問題への挑戦
などを 1 対 1 で徹底指導し、数学の総合的な応用力を身につけていきます。
「空間図形の中の直角三角形が見つけられない…」「ピタゴラス数の計算でルートが残ると混乱する…」という方は、ぜひ一度ご相談ください!



コメント