こんにちは、Thumb up Cafe Blogへようこそ!
前回、「相似」とは「形は同じで、大きさが違う図形」だと学びましたね。相似の考え方は、面積や体積、そして長さを測れない線分を求めるための、強力な魔法の道具になります。
今回は、この相似の知識をさらに深め、相似比と面積比・体積比の関係、そして平行線と線分の比の定理という、応用問題で必ず使う二大ツールを徹底解説します!
1. 🔑 相似比と面積比・体積比の関係
相似な図形は、辺の長さだけでなく、面積や体積にも美しいルールがあります。
1-1. 面積比(2乗の関係)
相似な平面図形(三角形、四角形、円など)において、その面積の比は、相似比の2乗になります。
| 項目 | 関係 | 公式 |
|---|---|---|
| 相似比 | a : b | |
| 面積比 | a² : b² | 面積比 = (相似比)² |
【例】
相似比が 2:3 の2つの三角形があったとします。
- 辺の長さの比(相似比)→ 2:3
- 面積の比 → 2² : 3² = 4 : 9
理由:
面積は「底辺 × 高さ ÷ 2」で求まります。相似比が a:b であれば、底辺も a:b、高さも a:b になります。
(a × a) : (b × b) = a² : b²
1-2. 体積比(3乗の関係)
相似な立体図形(立方体、円錐、球など)においては、その体積の比は、相似比の3乗になります。
| 項目 | 関係 | 公式 |
|---|---|---|
| 相似比 | a : b | |
| 体積比 | a³ : b³ | 体積比 = (相似比)³ |
【例】
相似比が 1:2 の2つの円錐があったとします。
- 辺の長さの比(相似比): 1:2
- 体積の比: 1³ : 2³ = 1 : 8
2. 📏 平行線と線分の比の定理:見えない長さを測るカギ
相似の知識は、図形の一部に平行線があるとき、辺の比を求める強力な武器になります。
2-1. 三角形と平行線(ピラミッド型と砂時計型)
三角形の中に、底辺と平行な線が引かれている場合、必ず相似な三角形ができます。
🔑 定理 1-A:辺の比は平行線で分けられる
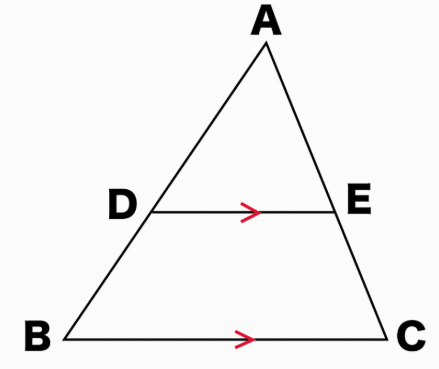

ポイント: 1. は小さい三角形と全体の三角形の相似比を表します。2. は途中の辺が平行線で分けられる比を表し、こちらの方が計算ミスが少ないことが多いです。
🔑 定理 1-B:砂時計型(交差型)

2-2. 平行線に交わる線分(拡張版)
3本以上の平行線に、2本の線分(横断線)が交わっている場合にも、辺の比のルールが成り立ちます。
🔑 定理 2:線分の比は等しい
3本以上の平行線が、2本の直線と交わるとき、2本の直線が平行線によって区切られる線分の比は等しくなります。

3. 🎯 Thumb up Cafe の個別指導で応用問題を突破!
相似の知識は、一見複雑な図形や、錐(すい)や柱(ちゅう)を途中で切断したような立体図形の問題で力を発揮します。特に「面積比や体積比」の問題は、相似比を正しく見抜けるかがカギとなります。
🚀 ブログだけでは物足りない、個別最適な学習サポートが必要な方へ
Thumb up Cafe のオンライン個別指導では、
- 相似比と比の定理を使った、補助線なしでの辺の長さの瞬間計算トレーニング
- 相似比の2乗・3乗を正確に応用し、面積・体積を求める演習
- 台形や複雑な多角形に隠された相似な三角形を見つけ出す訓練
などを 1 対 1 で徹底指導し、図形への苦手意識を強みに変えていきます。
「面積比と体積比をいつも間違える…」「平行線と線分の比の使い方が混乱する…」という方は、ぜひ一度ご相談ください!



コメント