こんにちは、Thumb up Cafe Blogへようこそ!
中学3年生の図形分野で学ぶ「相似(そうじ)」は、一見すると難しそうですが、実は私たちが日常で使う地図やスマートフォンの画面の拡大・縮小と同じ考え方です。
相似を理解することは、ピラミッドの高さや手の届かない距離を測る知恵にもつながります。今回は、この相似の定義と、証明の土台となる三角形の相似条件3つの秘密を徹底解説します!
1. 🌈 相似の定義: 形は同じ、大きさは違う
1-1. 相似とは?
相似とは、「一方の図形を一定の割合で拡大(または縮小)すると、もう一方の図形にぴったり重なること」をいいます。
合同が「形も大きさも全く同じ」だったのに対し、相似は「形は同じだが、大きさは違っても良い」という関係です。
1-2. 相似な図形のルール
2つの図形が相似であるとき、以下の2つのルールが成り立ちます。
- 対応する角の大きさは、それぞれ等しい。
- 対応する辺の長さの比(相似比)は、すべて等しい。
数学では、三角形 ABC と三角形 DEF が相似であることを、「△ ABC ∽ △ DEF」と、ニョロニョロの記号(相似記号)を使って表します。
相似な図形 ⇔ 角が等しく、辺の比が一定
2. 🔑 三角形の相似条件: 3つの強力なカギ
合同と同様に、相似もすべての辺の比とすべての角の等しさを確認する必要はありません。以下の3つの条件のうち、どれか一つが満たされれば、その2つの三角形は相似であると言えます。
🔑 条件 1: 3組の辺の比がすべて等しい(辺・辺・辺)
3 組の辺の比がすべて等しい。
- イメージ: 3つの辺の長さの比率(例: 1:2:3)が同じであれば、その辺で作られる三角形の形は1通りに決まります。大きさは違っても、形は同じです。
- 例:AB:DE=BC:EF=AC:DF
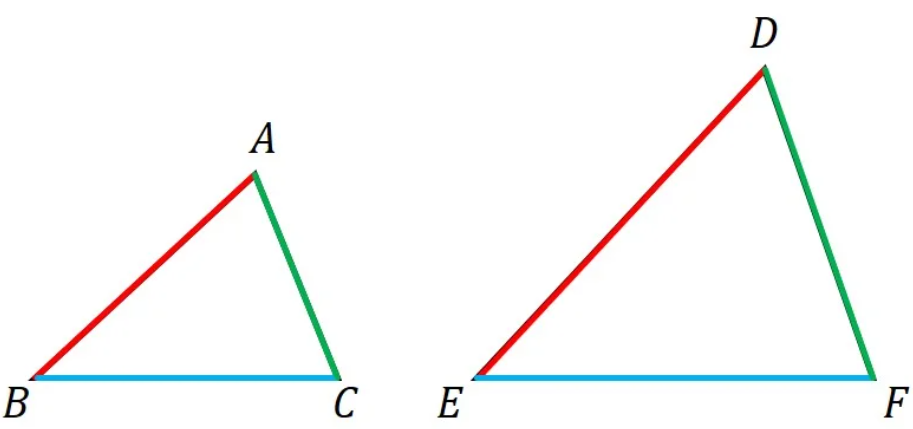
🔑 条件 2: 2組の辺の比とその間の角がそれぞれ等しい(辺・角・辺)
2 組の辺の比とその間の角がそれぞれ等しい。
- ポイント: 比が等しい2つの辺と、その2辺に挟まれた角が等しい必要があります。挟む角の大きさが決まれば、残りの辺の長さの比も自然と決まります。
- 例: AB:DE = BC:EF であり、かつ ∠ B = ∠ E ならば、相似です。
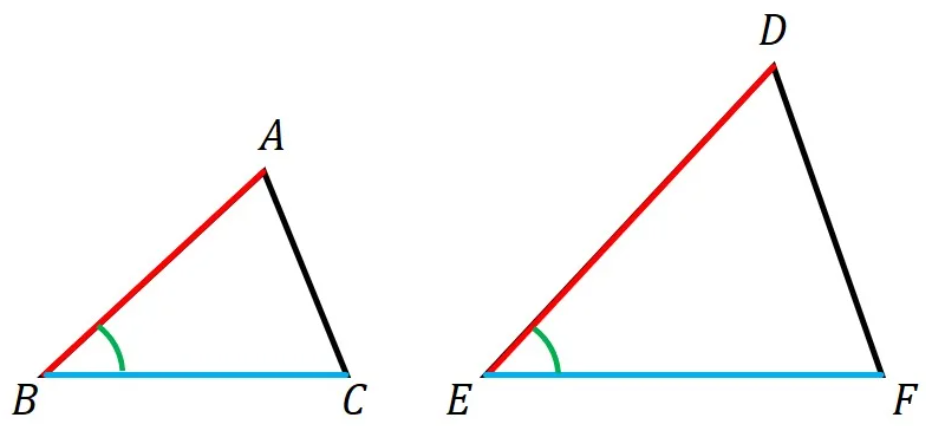
🔑 条件 3: 2組の角がそれぞれ等しい(角・角)
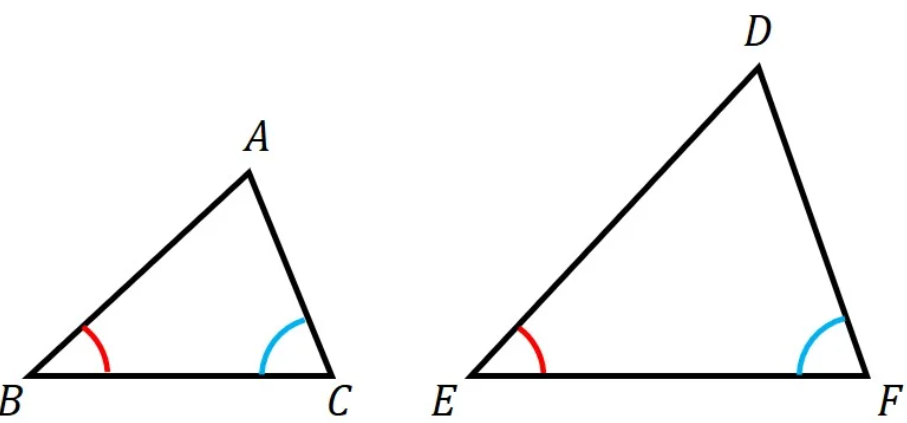
2 組の角がそれぞれ等しい。
- 最もよく使う条件です。三角形の内角の和は 180° ですから、2組の角が等しければ、残りの1組の角も自動的に等しくなります。
- ポイント: 辺の情報がなくても、角度の情報だけで相似を証明できます。
- 例:∠B = ∠E , ∠C = ∠F
3. 🧩 合同と相似のつながり
相似条件は、合同条件と非常によく似ています。
- 合同条件 1(SSS) → 3組の辺の長さが等しい(比が 1:1)
- 相似条件 1(SSS) → 3組の辺の比が等しい(比が a:b)
合同は、相似の中でも相似比が 1:1 の特別バージョンと考えることができます。
💡 相似証明への応用
相似の証明問題でも、合同の証明と同じく、問題文に書かれていない「隠れた情報」を使うことが重要です。
- 対頂角(たいちょうかく):2つの直線が交わっているとき、向かい合う角は必ず等しい。
→ 条件3(2組の角)を成立させるのに必須。 - 平行線の性質:錯角(Z の字)や同位角(F の字)が等しい。
→ 角度の情報を補うのに必須。 - 共通な角:2つの三角形が1つの角を共有している。
→ 条件2や条件3を成立させるのに必須。
4. 🎯 Thumb up Cafe の個別指導で相似を応用しよう!
相似の知識は、三平方の定理や円周角の定理と組み合わさって、入試で最も難易度の高い図形問題の土台となります。相似の概念をしっかり理解すれば、遠いものの大きさを計算する楽しさもわかってきます。
🚀 ブログだけでは物足りない、個別最適な学習サポートが必要な方へ
Thumb up Cafe のオンライン個別指導では、
- 「隠れた相似」を見つけるための、図形の読み解き方
- 相似比と面積比(相似比の2乗)や体積比(相似比の3乗)の応用計算
- 補助線を必要とする複雑な相似証明への挑戦
などを 1 対 1 で徹底指導し、図形の応用力を身につけていきます。
「相似条件がどれに当てはまるか迷う…」「複雑な図形になると相似な三角形が見つけられない…」という方は、ぜひ一度ご相談ください!



コメント