こんにちは、Thumb up Cafe Blogへようこそ!
中学3年生の数学で、二次関数 y=ax²という新しいタイプの関数に出会います。一次関数のグラフがまっすぐな直線だったのに対し、二次関数のグラフは美しい曲線を描きます。
この曲線が持つ性質と、それを読み解くための比例定数 a の秘密、そして変域(へんいき)の求め方を徹底的に解説します!
1. 🌈 二次関数の基本: y=ax² とは?
関数とは、「x の値が決まると、それに対応して y の値がただ一つに決まる関係」のことでした。
二次関数は、y が x の2乗に比例する形で表され、その基本の形は以下の通りです。
y=ax²
🔑 二次関数の特徴
- x が x² になる: x にプラスの数を入れてもマイナスの数を入れても、2乗されるため、y の値は急激に変化します。(例外: a が負の数の場合)
- 原点を通る: x=0 を代入すると、必ず y=a×0²=0 になるため、グラフは必ず原点 (0,0) を通ります。
2. 🎢 グラフの形:放物線(ほうぶつせん)の秘密
y=ax2 のグラフは、物を放り投げたときの軌跡のような左右対称の曲線になります。これを「放物線」と呼びます。
2-1. 頂点(ちょうてん)と軸(じく)
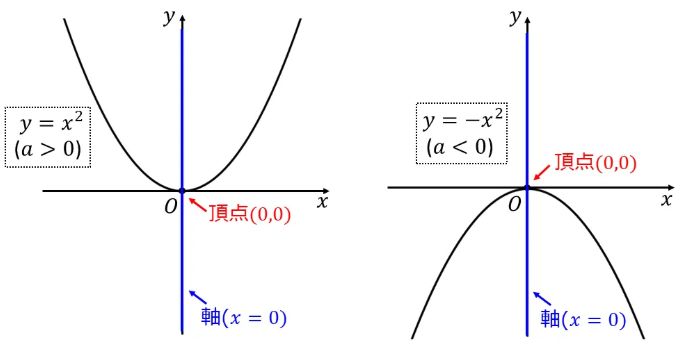
- 頂点: グラフの最も低い点、または最も高い点のことです。二次関数 y=ax² の頂点は、必ず原点 (0,0) になります。
- 軸: グラフを左右対称に分ける直線のことです。二次関数 y=ax² の軸は、必ずy 軸(直線 x=0)になります。
2-2. 比例定数 a の秘密:向きと開き方
グラフの形は、式の中の比例定数 a がすべて決めています。
| a の符号 | グラフの向き | 特徴 |
|---|---|---|
| a>0 (プラス) | 上に開く(下に凸) | 頂点が最も低い点(最小値)。U 字型。 |
| a<0 (マイナス) | 下に開く(上に凸) | 頂点が最も高い点(最大値)。逆 U 字型。 |
また、∣a∣ (a の絶対値)の大きさが、放物線の開き方を決定します。
- ∣a∣ が大きい(例: y=5x²) → 開きが狭い(細い)
- ∣a∣ が小さい(例: y=1/5x²) → 開きが広い(太い)
3. 🎯 変域の極意:グラフを見て最大・最小を判断する
変域とは、x の範囲(定義域)と、それに対応して y がとる値の範囲(値域)のことです。一次関数の変域は、両端の値を代入すれば求まりましたが、二次関数ではそうとは限りません。
二次関数の変域を求めるときは、「必ずグラフを描くこと」が極意です。
🔑 変域を求める2つのパターン
パターン 1: x の変域に 0 が含まれない場合
(例: 1≤x≤3 や −4≤x≤−2 など)
- 放物線は、頂点(x=0)を通りません。
- 一次関数と同様に、x の両端の値を代入したときの y の値が、そのまま y の変域の両端になります。
パターン 2: x の変域に 0 が含まれる場合(最重要!)
(例: −2≤x≤3 や −5≤x≤1 など)
このとき、グラフは必ず頂点 (0,0) を通ります。
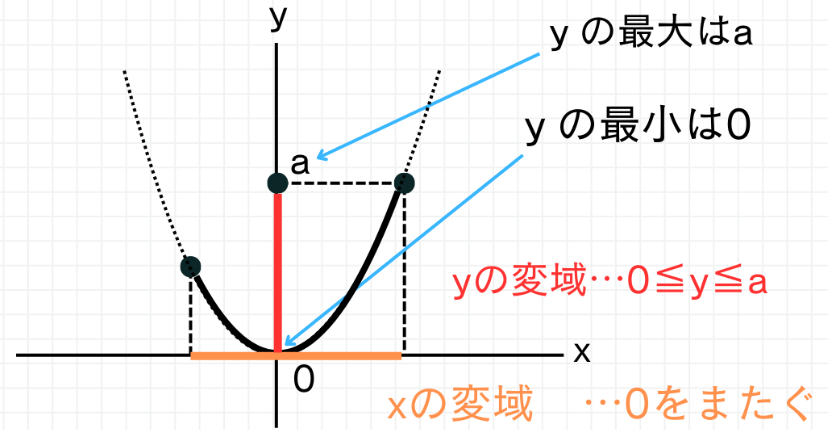
- a>0 (上に開くグラフ)の場合:
- 最小値は必ず頂点である y=0 になります。
- 最大値は、x の変域の両端のうち、絶対値が大きい方の x を代入して求めます。
- a<0 (下に開くグラフ)の場合:
- 最大値は必ず頂点である y=0 になります。
- 最小値は、x の変域の両端のうち、絶対値が大きい方の x を代入して求めます。
間違いやすい例: y=2x² で −3≤x≤1 のとき、
- x=−3 を代入 →y=18
- x=1 を代入 →y=2
- 最小値は原点 y=0 0≤y≤18
4. 🎯 Thumb up Cafe の個別指導でグラフを味方に!
二次関数の学習は、この後で学ぶ二次方程式の解の個数や三平方の定理の理解に直結します。特に変域の問題は、グラフのイメージさえあれば決して間違えません。
🚀 ブログだけでは物足りない、個別最適な学習サポートが必要な方へ
Thumb up Cafe のオンライン個別指導では、
- a の値の決定(グラフ上の点から式を求める)のパターン演習
- 変域の問題で 0 を含む場合の最小値・最大値を瞬時に判断するトレーニング
- 二次方程式の解をグラフの交点として理解する応用学習
などを 1 対 1 で徹底指導し、二次関数を得点源に変えていきます。
「変域の問題になるといつも 0 を入れ忘れる…」「 a の符号とグラフの向きが混乱する…」という方は、ぜひ一度ご相談ください!



コメント