こんにちは、Thumb up Cafe Blogへようこそ!
中学3年生の数学で、皆さんの前に現れる新しい記号が「√ (ルート)」です。この記号を使った計算、すなわち「平方根(へいほうこん)」の学習は、二次方程式や三平方の定理といった、これからの数学の応用分野を理解するための土台となります。
今回は、この平方根の定義から、計算を楽にするための有理化(ゆうりか)、そしてルートの計算ルールを徹底解説します!
1. 🌈 平方根の定義: 2乗すると a になる数
1-1. 平方根とは?
平方根とは、「2乗すると a になる数」のことです。
例えば、「2乗すると 9 になる数」を考えてみましょう。
- 3 × 3 = 9 ですから、3 は 9 の平方根です。
- (-3) × (-3) = 9 ですから、-3 も 9 の平方根です。
ポイント:
正の数 a の平方根は、必ず正の数と負の数の 2 つあります。
1-2. 根号(√:ルート)の導入
しかし、「2乗すると 2 になる数」は、きれいな整数や分数では表せません。そこで、この数を表すために特別な記号が使われます。これが「根号(こんごう)」あるいは「ルート」と呼ばれる √ です。
2 の平方根は、 √2 と -√2
- √2 は、2乗すると 2 になる正の数(約 1.414)を表します。
- √ の中の数は常に 0 以上でなければなりません。(2乗して負の数になる数はありません)
2. 🔑 根号のルール:乗法・除法(かけ算・わり算)
ルート同士のかけ算・わり算は、中の数(根号の中の数)同士で計算できます。
🔑 公式 1:乗法(かけ算)
ルートの中の数同士をかけ算し、1つのルートにまとめられます。
√a × √b = √ab
- 例: √3} × √5 = √3 × 5} = √15
🔑 公式 2:除法(わり算)
ルートの中の数同士でわり算し、1つのルートにまとめられます。
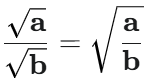
- 例:
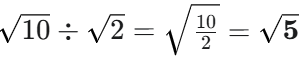
🔑 公式 3: a√b の形への変形(aを中に入れる/外に出す)
ルートの中の数が2乗になっている部分があれば、それをルートの外に出すことができます。逆に、外にある数は、2乗して中に入れることができます。
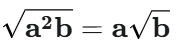
- 例(外に出す):
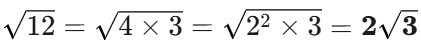
- 例(中に入れる):
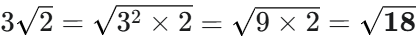
3. 🧩 計算の工夫:有理化(ゆうりか)
有理化とは、「分母に根号(ルート)がない形」にすることです。なぜなら、分母にルートがあると、その後の計算が複雑になったり、答えを比べるのが難しくなったりするからです。
💡 有理化の基本ルール
分母にある √a を消すために、分母と分子の両方に、同じ √a をかけます。
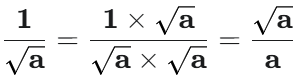
- 分母と分子に同じ数をかけても、値は変わらないという性質(分数の性質)を利用しています。
- 例:
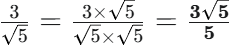
4. ➕ 根号を含む式の計算:加法・減法(たし算・ひき算)
たし算・ひき算は、かけ算・わり算とルールが異なります。
🔑 ルール: ルートの中が同じものだけ計算できる!
たし算・ひき算は、ルートの中の数(被開平数)が全く同じであるものだけが計算できます。これは、文字式で同類項をまとめるのと同じルールです。
a√M + b√M = (a + b)√M
- 例: 3√5 + 4√5 = (3+4)√5 = 7√5
- できない例: √2 + √3 は、ルートの中が異なるため、これ以上計算できません。
🔑 総合計算のステップ
複雑な式は、必ず以下の手順で計算しましょう。
- 変形(外に出す): ルートの中の数をできるだけ小さく変形し(√12 → 2√3 など)、ルートの中を統一します。
- 有理化: 分母にルートがあれば、有理化します。
- 計算: ルートの中が同じもの(同類項)だけを、たし算・ひき算します。
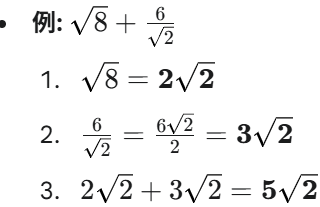
5. 🎯 Thumb up Cafe の個別指導で計算を自動化しよう!
平方根の計算は、ミスなく正確に、そして速く処理する「計算力」が問われます。特に、変形と有理化を瞬時に行う訓練が必要です。
🚀 ブログだけでは物足りない、個別最適な学習サポートが必要な方へ
Thumb up Cafe のオンライン個別指導では、
- √a²b = a√b の変形と有理化を自動的に行えるようにする徹底訓練
- 平方根の近似値(√2 ≒ 1.414 など)と、数の大きさの理解
- 二次方程式や三平方の定理での平方根の応用問題へのスムーズな移行
などを 1 対 1 で徹底指導し、平方根計算を確実な得点源に変えていきます。
「有理化と変形の順序が混乱する…」「たし算とひき算のルールがうろ覚えだ…」という方は、ぜひ一度ご相談ください!



コメント