こんにちは、Thumb up Cafe Blogへようこそ!
中学2年生の数学で、皆さんの目の前に現れるのが「一次関数」です。難しそうに見えますが、実は世の中の多くの規則的な変化を表す、とても便利なツールなんです。
今回は、この一次関数の「魔法の式」である y=ax+b の意味をしっかりと理解し、グラフを描けるようになるまでを徹底的に解説していきます!
1. 🌈 一次関数の「基本の形」: y = ax + b
関数とは、「一方の数が決まると、もう一方の数がただ一つに決まる関係」のことです。一次関数は、必ず次のまっすぐな形(一次)で表されます。
y = ax + b
この式を理解するために、身近な例として「タクシーの料金」を考えてみましょう。
| 文字・定数 | 名称 | タクシー料金での役割 |
|---|---|---|
| x | 変数 | 走った距離(km) → 原因となる数 |
| y | 変数 | 合計の料金(円) → 結果となる数 |
| a | 傾き | 1kmごとに増える追加料金 → 変化のスピード |
| b | 切片 | 最初に必ずかかる初乗り料金 → スタート地点 |
💡 式の構造を分解!
タクシーの料金は、次のように計算されています。
合計料金 = (追加料金) + (初乗り料金)
y = a × x + b
つまり、一次関数の式は、「変化のスピード (a) でどんどん変わる部分」と、「最初に決まっている部分 (b)」の足し算でできているのです。
2. 🗻 傾き a と 切片 b の秘密
一次関数のすべては、この2つの数(aとb)に詰まっています。
2-1. 傾き a: 変化のスピード(グラフの坂の急さ)
傾き a は、xが1増えたときに、yがどれだけ増えるかを表しています。数学では「変化の割合」とも呼びます。
グラフで考えると、この傾き a が、直線の坂道の急さ(角度)を決めています。

- a がプラス:グラフは右上がり(上り坂)になります。
- a がマイナス:グラフは右下がり(下り坂)になります。
- a の絶対値が大きい:坂が急で、変化のスピードが速いことを意味します。
2-2. 切片 b: グラフのスタート地点
切片 b は、グラフがタテの線(y軸)とぶつかる場所の座標です。
これは、式に x = 0 を代入したときの y の値、つまり「何も始まっていない状態(x=0)のときの y の初期値」を意味します。
切片 b は、グラフ全体の位置を上下に移動させる役割を持っています。
3. 🗺️ 一次関数のグラフの描き方: 2つの数字で直線を引く!
一次関数のグラフは、必ず直線になります。この直線を引くには、たった2つの点さえ分かれば十分です。最も簡単な描き方は、切片と傾きを使う方法です。
✍️ グラフ作成の3ステップ
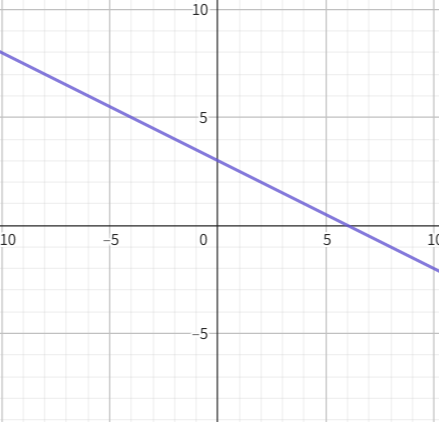
例: ![]() のグラフを描いてみましょう。
のグラフを描いてみましょう。
| 手順 | 内容 | グラフ上の動き |
|---|---|---|
| 1. 切片 b でスタート地点を決める | 切片 b は +3 です。タテの線(y軸)上の 3 の場所に最初の点 (0, 3) を打ちます。 | スタート地点 |
| 2. 傾き a で次の点を決める | 傾き a は -1/2 です。 → ヨコに 2 進むと、タテに 1 下がる(マイナスだから)という意味。 | 進み方 |
| 3. 2点を結び、直線を引く | 手順1の点からスタートし、右に2マス、下に1マス進んだ場所に2つ目の点を打ちます。この2点を定規でまっすぐにつなぎます。 | 直線が完成 |
4. 🎯 Thumb up Cafe の個別指導でグラフの応用力を磨こう!
一次関数は、この後で学習する図形や、連立方程式と密接に結びついてきます。特に、グラフの交点を求める問題や、図形の面積を関数で考える問題は、入試でも頻出の応用テーマです。
一次関数を完全に理解すれば、グラフを見て式が書け、式を見てグラフが描けるという、数学的な思考力が身につきます。
🚀 ブログだけでは物足りない、個別最適な学習サポートが必要な方へ
Thumb up Cafe のオンライン個別指導では、グラフの基本的な描き方から、
- 2直線の交点を求める連立方程式の応用
- 面積を2等分する直線の式を求める問題
まで、複雑なグラフの応用問題も 1 対 1 で徹底指導します。
「グラフの読み取りや応用問題が苦手…」という方は、ぜひ一度ご相談ください!


コメント