はじめに:連立方程式って、なんだろう?
中学2年生の数学で、新しい壁として立ちはだかるのが連立方程式です。
連立方程式(正式には連立二元一次方程式)とは、文字が2つ(xとyなど)含まれている一次方程式を2つ組み合わせたものです。この2つの式を同時に成り立たせるような、xとyの一組の値を見つけることが目標となります。
例えば、
- 「りんご1個とみかん2個で、合計310円」 → x + 2y = 310
- 「りんご2個とみかん1個で、合計380円」 → 2x + y = 380
このように、現実の問題を解くために2つの文字(x:りんごの値段, y:みかんの値段)を使う必要が出てきます。これを解くための強力なツールが、これから学ぶ加減法と代入法の2つです!
1. 連立方程式の基本:ゴールは「文字を1つに減らす」こと!
連立方程式を解くための最も重要な考え方は、2つある文字のうち、どちらか一方を消去して、文字が1つだけの一次方程式(xだけ、またはyだけの式)にしてしまうことです。
文字が1つになれば、中1で習った一次方程式の知識で簡単に解くことができます。
その「文字を消す」ための具体的なテクニックが、「加減法」と「代入法」なのです。
2. 🤖 加減法(かげんほう)で解く:足し算・引き算で文字を消す
加減法は、連立方程式を解くための最も一般的な方法です。2つの式をそのまま足したり引いたり(加減)することで、特定の文字を消去します。
📝 加減法の基本的な手順
- 消したい文字を決める:xとyのどちらを消すか決めます。
- 係数を揃える:消したい文字の係数の絶対値が揃っているか確認します。
- 揃っていない場合は、式全体に数をかけて係数を揃えます。(例:2yと3yを消すなら、一方の式を3倍、もう一方の式を2倍して6yにする)
- 式を足すか引くか決める:
- 係数の符号が同じ(+2yと+2yなど) → 引く
- 係数の符号が違う(+2yと-2yなど) → 足す
- 文字が1つになった方程式を解く:残った文字の値を求めます。
- 代入して、もう一方の文字の値を求める:手順4で求めた値を、元の式のどちらかに代入し、もう一つの文字の値を求めます。
🌟 例題と解説
例題1:
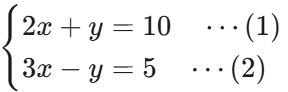
| 手順 | 説明 | 途中式 |
|---|---|---|
| 1. & 2. | yの係数は +1 と -1 で、絶対値が揃っている。 | – |
| 3. 足し算で y を消す | 符号が違うので、(1)式と(2)式を足す。 | (2x + y) + (3x – y) = 10 + 5 |
| 4. xの値を求める | yが消えて 5x = 15 となる。 | 5x = 15 → x = 3 |
| 5. yの値を求める | x=3を(1)式に代入。 | 2(3) + y = 10 → 6 + y = 10 → y = 4 |
答え: x=3, y=4
例題2:係数を揃える場合
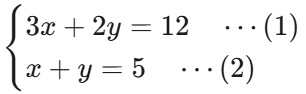
- 係数を揃える:今回はyを消去するために、(2)式を2倍します。
(2) × 2 → 2x + 2y = 10 … (2)’ - 引き算で y を消す: (1)式と(2)’式は yの係数が +2y と +2y で符号が同じなので、引く。
(1) – (2)’ → (3x + 2y) – (2x + 2y) = 12 – 10
x = 2 - 代入: x=2 を元の簡単な式 (2)に代入。
2 + y = 5 → y = 3
答え: x=2, y=3
3. ✍️ 代入法(だいにゅうほう)で解く:「すり替えて」文字を消す
代入法は、一方の式を「x= (ほかの文字の式)」または「y= (ほかの文字の式)」の形に変形し、それをもう一方の式に代入して文字を消去する方法です。
📝 代入法の基本的な手順
- 代入する式を準備する:どちらかの式を「x=・・・」または「y=・・・」の形に変形します。(既にこの形であれば省略)
- もう一方の式に代入する:変形した式を、代入する文字(xまたはy)の部分に(必ずかっこを付けて)代入します。
- 文字が1つになった方程式を解く:残った文字の値を求めます。
- 代入して、もう一方の文字の値を求める:手順3で求めた値を、変形した式(手順1の式)に代入するのが最も簡単です。
🌟 例題と解説
例題3:
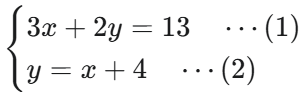
| 手順 | 説明 | 途中式 |
|---|---|---|
| 1. 準備 | (2)式は既に「y = ・・・」の形になっている。 | – |
| 2. 代入 | (2)を(1)の y の部分に代入する。必ずかっこを付ける。 | 3x + 2(x + 4) = 13 |
| 3. xの値を求める | かっこを外し、一次方程式として解く。 | 3x + 2x + 8 = 13 → 5x = 5 → x = 1 |
| 4. yの値を求める | x=1を簡単な (2)式に代入。 | y = 1 + 4 → y = 5 |
答え: x=1, y=5
4. 💡 成功の鍵!加減法と代入法の使い分け
連立方程式は、どちらの方法を使っても必ず同じ答えが出ます。しかし、問題の形に合わせて最適な方法を選ぶことで、計算ミスを防ぎ、素早く解くことができます。
| 解き方 | 適している問題の特徴 |
| 加減法 | 文字の係数が、比較的簡単に揃えられる場合。(例:2xと3x、-yとyなど)連立方程式の大多数はこの解き方で解けます。 |
| 代入法 | 既に「x = ・・・」や「y = ・・・」の形になっている場合。または、文字の係数が +1 や -1 の項がある場合。 |
迷ったら、まずは 加減法 を試してみるのが基本です!
応用問題へのステップ
連立方程式には、今回解説した基本形以外にも、かっこを含むものや、分数・小数が含まれるものがありますが、これらも基本は同じです。
- かっこを外す
- 分数・小数を整数係数に直す(両辺に10や100、または分母の最小公倍数をかける)
- 加減法または代入法で解く
このステップを踏めば、どんな連立方程式も解くことができます。
5. まとめと次のステップ
連立方程式は、文字を1つに減らすという共通の目的を、加減法と代入法という2つの方法で達成します。
- 加減法:足し引きで文字を消す。係数を揃えるのがポイント。
- 代入法:「x=」の形にして、もう一方の式に代わりに入れる。
まずは、基本の例題を完璧に解けるように繰り返し練習しましょう。
| 問題形式 | 解き方 |
|---|---|
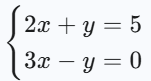 | 加減法(yの係数が揃っている) |
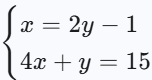 | 代入法(xが既に分離されている) |
さあ、次のステップへ!
基本問題が解けるようになったら、今度は「お菓子を買う」「速さ・時間・道のり」といった文章問題に挑戦してみましょう。文章を読んで連立方程式を立てることが、連立方程式マスターへの最終課題です!
🚀 ブログだけでは物足りない、個別最適な学習サポートが必要な方へ
Thumb up Cafe のオンライン個別指導では、
- 連立方程式の文章問題からの正確な立式
- 一次関数のグラフの交点を求める応用問題への取り組み方
などを 1 対 1 で徹底指導し、あなたの数学のつまずきを解消します。
「文章から式を立てるのが苦手…」「応用問題でいつも手が止まる…」という方は、ぜひ一度ご相談ください!


コメント