こんにちは、Thumb up Cafe Blogへようこそ!
中学2年生の図形分野で登場する「平行線と角」「合同」は、一見複雑そうに見えますが、実は数少ないシンプルなルールで成り立っています。このルールを知っているかどうかで、入試問題の難易度が大きく変わると言っても過言ではありません。
今回は、図形の世界に隠された角の魔法と合同の秘密を解き明かし、証明問題の土台となる基礎を徹底解説します!
1. 📏 平行線と角の基本:3つの角の仲間
2本の直線が平行なとき、そこに1本の直線(横断線)が交わると、8つの角が生まれます。この8つの角には、特別な関係を持つ3組の仲間がいます。
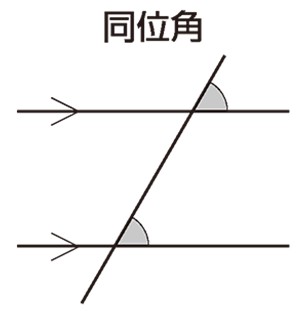
1-1. 🤝 同位角(どういかく): 同じ位置の仲間
同位角とは、交わる線に対して、同じ位置(方向)にある角のことです。
- ルール: 2つの直線が平行である場合、同位角は必ず等しくなります。また、同位角が等しければ、2つの直線は平行です。
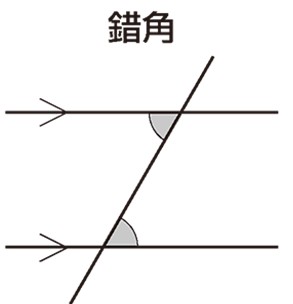
1-2. 🔄 錯角(さっかく): ZまたはNの字の仲間
錯角とは、横断線に対して反対側、かつ2つの平行線に挟まれた内側(内角)にある角のことです。形で見ると、ちょうどアルファベットの「Z」の形になります。
- ルール: 2つの直線が平行である場合、錯角は必ず等しくなります。また、錯角が等しければ、2つの直線は平行です。
2. 🔺 三角形の内角・外角の秘密
平行線のルールは、三角形や多角形の性質を解き明かすカギにもなります。
2-1. 三角形の内角の和は 180°
三角形の3つの内角(内側にある角)の合計は、いつでも 180° です。
これは、三角形の頂点を通る補助線を底辺と平行に引くことで、錯角の性質を使って証明できます。
2-2. 多角形の内角・外角の和
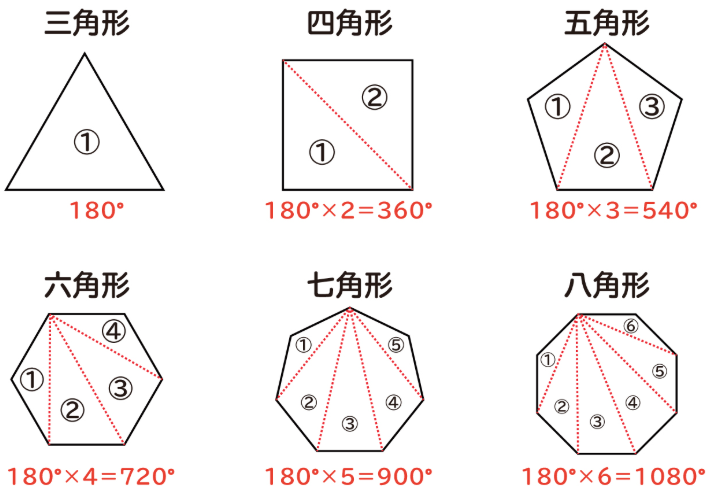
- 多角形の内角の和: n角形は、一つの頂点から対角線を引くことで (n – 2) 個の三角形に分かれます。
(n 角形の内角の和) = 180° × (n – 2)
- なお、多角形の外角の和は、
→ 多角形の形や辺の数に関係なく、かならず360°になります。
3. 👯♀️ 図形の合同(ごうどう)とは?
「合同」とは、2つの図形がぴったりと重ね合わせられることを言います。見た目も形も、すべて同じであるということです。
合同な図形では、対応する辺の長さはすべて等しく、対応する角の大きさもすべて等しくなります。
🔑 三角形の合同条件
合同を証明するには、すべての辺と角が等しいことを示す必要はありません。以下の3つの条件のうち、どれか一つが満たされれば、その2つの三角形は合同であると言えます。
| 合同条件 | 説明 | 必要な情報 |
| 1. 3組の辺がそれぞれ等しい | 3つの辺の長さが、すべて対応する辺と等しい。 | 辺・辺・辺 (SSS) |
| 2. 2組の辺とその間の角がそれぞれ等しい | 2つの辺の長さと、その2辺に挟まれた角の大きさが等しい。 | 辺・角・辺 (SAS) |
| 3. 1組の辺とその両端の角がそれぞれ等しい | 1つの辺の長さと、その辺の両端にある2つの角の大きさが等しい。 | 角・辺・角 (ASA) |
4. 🧩 平行線と角の性質が合同証明に役立つ!
合同の証明問題では、一見情報が足りないように見えても、先に学んだ「平行線と角の性質」を使うことで、足りない「角」の情報を補うことができます。
【合同証明への応用例】
- 「Z の字」で角を補う:問題文に「直線 AB // CD」のように平行線が与えられていれば、横断線に対する錯角が等しい(例: ∠ BAC = ∠ DCA)ことを証明に使うことができます。
- 「対頂角(たいちょうかく)」を使う:2つの直線が交わるとき、向かい合う角は必ず等しい(対頂角は等しい)というルールも、合同条件の「角」を埋めるのに頻繁に使われます。
このように、平行線と角のルールは、図形を読み解き、合同条件を成立させるための重要なステップとなるのです。
5. 🎯 Thumb up Cafe の個別指導で証明問題を突破!
合同の証明問題は、「どこから手をつけたらいいか分からない」という声を多く聞きますが、実は手順とルールが決まっています。図形の応用問題は、この合同証明を土台として構成されています。
🚀 ブログだけでは物足りない、個別最適な学習サポートが必要な方へ
Thumb up Cafe のオンライン個別指導では、
- 図形が合同であることの論理的な道筋(手順)の作成指導
- 錯角・同位角・対頂角など、証明に必要な根拠の正確な使い方
- 合同条件(SSS, SAS, ASA)を素早く見抜くための図形の読み方
などを 1 対 1 で徹底指導し、証明問題への苦手意識を強みに変えていきます。
「合同の証明でいつも手が止まる…」「角の根拠を見つけられない…」という方は、ぜひ一度ご相談ください!



コメント