こんにちは、Thumb up Cafe Blogへようこそ!
中学2年生の数学で、サイコロやコイン、くじ引きなどの身近な現象を扱う「確率(かくりつ)」を学習します。確率は、ギャンブルだけでなく、統計やAIなど、未来を予測するための論理的な思考力を養う、とても面白い分野です。
今回は、確率を計算するための土台となる「場合の数(ばあいのかず)」の数え方と、情報を整理する強力なツール「樹形図(じゅけいず)」の書き方を徹底解説します!
1. 🌈 確率の定義: 予測を数値化する魔法の式
「確率は 50% だね」という言葉は日常でも使いますが、数学では確率を分数で表します。
確率とは、「全部で起こり得る結果のうち、特定の出来事が起こる割合」を数値化したものです。
💡 確率の基本公式
確率は、次のシンプルな公式で計算できます。

【例:コイン投げ】
コインを1回投げるとき、「表」が出る確率は?
- 起こり得るすべての場合の数: 「表」と「裏」の2通り。
- その出来事(表)の起こる場合の数: 1通り。

🔑 大原則: 「同様に確からしい」
確率を考える上で最も重要なのは、「どの結果も、同じように起こりやすい(同様に確からしい)」と考えることです。もしサイコロが歪んでいて特定の目が出やすくなっている場合、この公式は使えません。
2. 🔢 場合の数: 漏れなく重複なく数える技術
確率を求めるためのカギは、分母と分子にある「場合の数」を正確に数えることです。数え方に慣れていないと、「数え漏れ」や「重複して数える」というミスが起こりやすくなります。
2-1. 同時または連続で起こる場合の数
2つ以上の出来事が同時に、または連続して起こる場合の数は、「積の法則(かけ算)」で求められることが多いです。
| 問題 | 計算 | 結果(場合の数) |
|---|---|---|
| コインを 2枚 投げる | 1枚目(2通り) × 2枚目(2通り) | 4通り |
| 大小 2つのサイコロを投げる | 大(6通り) × 小(6通り) | 36通り |
| 3種類の服と2種類のズボンから 1着ずつ選ぶ | 服(3通り) × ズボン(2通り) | 6通り |
2-2. 順番に関わる場合の数(並べ方)
いくつかのものを一列に並べる場合の数も、かけ算で求められます。
【例:3人を並べる】
A、B、Cの3人が一列に並ぶ場合の数は?
- 1番目: 3人のうち誰でも選べる → 3通り
- 2番目: 残りの2人から選べる → 2通り
- 3番目: 最後の1人 → 1通り
3 × 2 × 1 = 6 通り
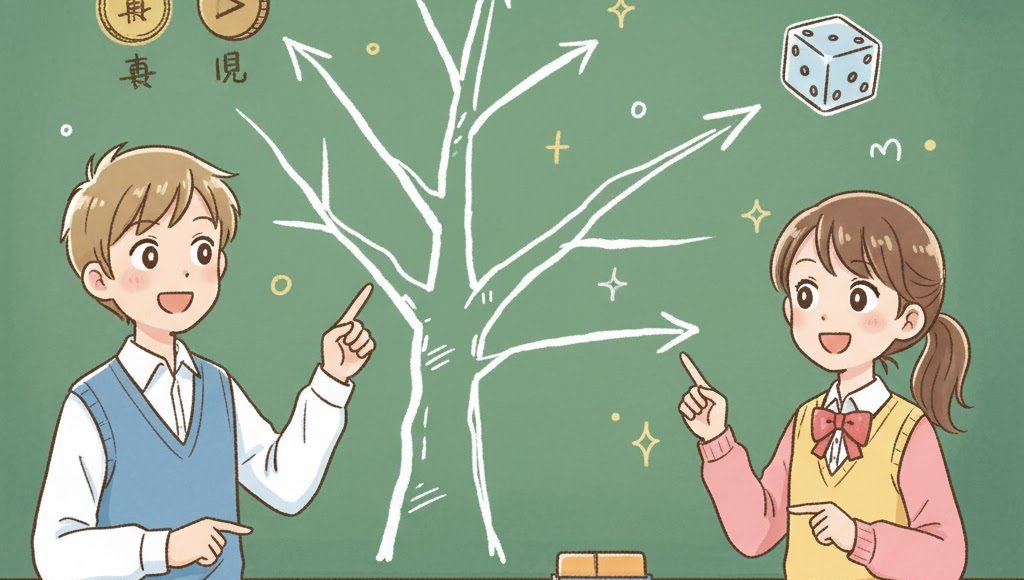
3. 🌲 樹形図(じゅけいず): 複雑な問題をシンプルにするツール
樹形図は、「すべての場合の数」を漏れなく、重複なく数えるための強力な図解ツールです。特に、同時や連続で起こる出来事を数えるときに威力を発揮します。
樹形図は、「木の枝のように」結果を順番に書き出していくのが特徴です。
✍️ 樹形図の書き方(例:コイン2枚投げ)
コイン(A, B)を2枚投げる場合の結果(4通り)を樹形図で見てみましょう。
- 最初の出来事(コインAの結果)を幹として書く。
- 次の出来事(コインBの結果)を、最初の結果から枝分かれさせて書く。
- すべての枝の先をたどると、すべての場合の数が見つかります。
| 結果A | 結果B | 結果の組み合わせ |
|---|---|---|
| 表 | → 表 | (表, 表) |
| → 裏 | (表, 裏) | |
| 裏 | → 表 | (裏, 表) |
| → 裏 | (裏, 裏) |
4 通り
🌳 樹形図のメリット
- 漏れ・重複の防止: すべての結果を視覚的に確認できるため、数え間違いを防げます。
- 特定の事象の抽出: 「少なくとも1枚が表」など、問題で指定された事象(出来事)を、樹形図の中から数えやすくなります。(この場合、(表, 表), (表, 裏), (裏, 表) の 3通り)
4. 🎯 Thumb up Cafe の個別指導で確率を得点源に!
確率は、計算自体は難しくありませんが、「場合の数」を正確に捉えられるかどうかが勝負の分かれ目となります。問題が複雑になると、樹形図も大きく複雑になります。
🚀 ブログだけでは物足りない、個別最適な学習サポートが必要な方へ
Thumb up Cafe のオンライン個別指導では、
- 複雑な条件(「少なくとも」「〜でない」など)を含む場合の数の読み解き方
- 樹形図や表など、問題に応じた適切な整理方法の選び方
- 樹形図を使わずに、かけ算(積の法則)で効率よく場合の数を求める技術
などを 1 対 1 で徹底指導し、確率分野を得点源に変えていきます。
「複雑な樹形図のどこから書き始めればいいか迷う…」「文章題になると場合の数を数え間違える…」という方は、ぜひ一度ご相談ください!


コメント